大二那会根本没蹋下心来看,觉得天书一般,连旋转都没搞明白。
今天仔细看了书,发现真的一点不难啊,鄙视自己……
首先是概念:
平衡二叉树是为了解决前面二叉排序树不均衡的问题,而加入了一种平衡机制。所以,平衡二叉树是一种特殊的二叉排序树(BST)!
AVL树查找的平均和最差复杂度都是O(logn) !!!(BST的最坏是O(n))
AVL树的插入复杂度是O(logn)。
平衡二叉树(简称AVL树):对任意一个结点,它的左子树和又子树都是平衡二叉树(左子树都小于结点,右子树都大于结点),且左子树深度和右子树深度不超过1。
书上那个平衡因子的概念只是为了辅助书上的实现方法,没有太大意义。
一般是在AVL树的构造(插入)阶段,做树的平衡处理(左、右旋),使得它称为一个平衡二叉树。
可以证明,AVL树的深度是logN。
中序遍历AVL树(其实这是二叉排序树),可以从小到大还原出一个序列。
下面的图摘自董师兄的博客《数据结构之AVL树》
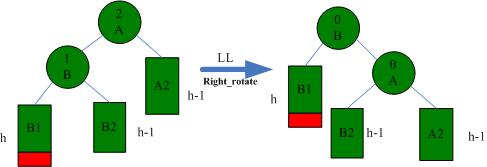
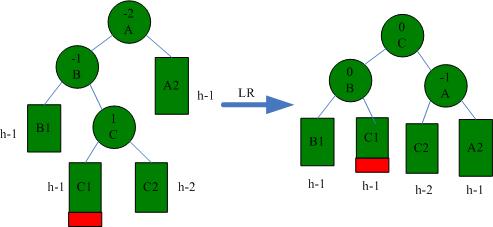
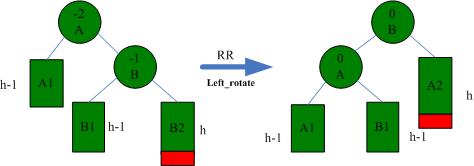
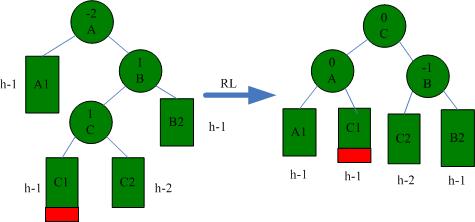
一般,我们在插入时会遇到4种不平衡情况:
(1)Insert在左子树的左子树,此时需要根右旋转。
(2)Insert在左子树的右子树,此时先要对左子树左旋转,然后对根右旋转。
(3)Insert在右子树的右子树,此时需要根左旋转。
(4)Insert在右子树的左子树,此时先要对右子树右旋转,然后对根左旋转。
我们的实现中,没有用平衡因子,而是直接记录每个结点子树的深度,如下:
public class AVLNode {
public AVLNode(int data) {
this.data = data;
}
public int data;
public AVLNode left = null;
public AVLNode right = null;
public int depth = 0;
}
为了方便处理null结点的深度,我们定义如下深度函数:
当空结点为-1时,它的父亲结点+1正好是0。
public static int Depth(AVLNode node) {
if (node == null) {
return -1;
} else {
return node.depth;
}
}
然后是左旋操作:
特别注意:更新结点时要先更新下面的(原tree结点),再更新新的mid。
返回要返回mid。
public static AVLNode RotateLeft(AVLNode tree) {
// Rotate right
AVLNode mid = tree.right;
tree.right = mid.left;
mid.left = tree;
// Update depth (Notify the sequence)
tree.depth = Math.max(Depth(tree.left), Depth(tree.right)) + 1;
mid.depth = Math.max(Depth(mid.left), Depth(mid.right)) + 1;
return mid;
}
同理,右旋操作:
public static AVLNode RotateRight(AVLNode tree) {
// Rotate left
AVLNode mid = tree.left;
tree.left = mid.right;
mid.right = tree;
// Update depth (Notify the sequence)
tree.depth = Math.max(Depth(tree.left), Depth(tree.right)) + 1;
mid.depth = Math.max(Depth(mid.left), Depth(mid.right)) + 1;
return mid;
}
好了,下面是插入的代码:
特别注意,Java中的引用实际是C++中的指针,即对函数传入的“临时变量”修改,将不会影响外围原变量!
因此,我们每次需要返回这个树引用。调用时也应该是
tree = Insert(tree, data);
public static AVLNode Insert(AVLNode tree, int data) {
if (tree == null) {
tree = new AVLNode(data);
} else {
if (data < tree.data) {
// Insert at left child
tree.left = Insert(tree.left, data);
if (Depth(tree.left) - Depth(tree.right) == 2) {
// Need balance
if (data < tree.left.data) {
// Insert at left child's left child
// Left-Rotate
tree = RotateRight(tree);
} else if (data > tree.left.data) {
// Insert at left child's right child
// First Left-rotate tree's left child
// Then Right-rotate tree
tree.left = RotateLeft(tree.left);
tree = RotateRight(tree);
}
}
} else if (data > tree.data) {
// Insert at right child
tree.right = Insert(tree.right, data);
if (Depth(tree.left) - Depth(tree.right) == -2) {
if (data > tree.right.data) {
// Insert at right child's right
// Left-Rotate
tree = RotateLeft(tree);
} else if (data < tree.right.data) {
// Insert at right child's left
// First Right-rotate on tree's right child
tree.right = RotateRight(tree.right);
// Then Left-rotate tree
tree = RotateLeft(tree);
}
}
}
}
// Update depth
tree.depth = Math.max(Depth(tree.left), Depth(tree.right)) + 1;
return tree;
}
查找和排序二叉树一样的,如下:
public static boolean Find(AVLNode tree, int key) {
AVLNode ptr = tree;
while (true) {
if (ptr == null) {
break;
}
if (key == ptr.data) {
return true;
} else if (key < ptr.data) {
ptr = ptr.left;
} else {
ptr = ptr.right;
}
}
return false;
}
好了,上面的版本有点土,用了Java还用static,下面这个版本是将AVLNode封装在了类内。调用时候不用在保存更新的AVLNode了,内部处理了,如下:
import java.util.Random;
public class AVLTree {
private int Depth(AVLNode node) {
if (node == null) {
return -1;
} else {
return node.depth;
}
}
private AVLNode RotateRight(AVLNode tree) {
// Rotate left
AVLNode mid = tree.left;
tree.left = mid.right;
mid.right = tree;
// Update depth (Notify the sequence)
tree.depth = Math.max(Depth(tree.left), Depth(tree.right)) + 1;
mid.depth = Math.max(Depth(mid.left), Depth(mid.right)) + 1;
return mid;
}
private AVLNode RotateLeft(AVLNode tree) {
// Rotate right
AVLNode mid = tree.right;
tree.right = mid.left;
mid.left = tree;
// Update depth (Notify the sequence)
tree.depth = Math.max(Depth(tree.left), Depth(tree.right)) + 1;
mid.depth = Math.max(Depth(mid.left), Depth(mid.right)) + 1;
return mid;
}
private AVLNode Insert(AVLNode tree, int data) {
if (tree == null) {
tree = new AVLNode(data);
} else {
if (data < tree.data) {
// Insert at left child
tree.left = Insert(tree.left, data);
if (Depth(tree.left) - Depth(tree.right) == 2) {
// Need balance
if (data < tree.left.data) {
// Insert at left child's left child
// Left-Rotate
tree = RotateRight(tree);
} else if (data > tree.left.data) {
// Insert at left child's right child
// First Left-rotate tree's left child
// Then Right-rotate tree
tree.left = RotateLeft(tree.left);
tree = RotateRight(tree);
}
}
} else if (data > tree.data) {
// Insert at right child
tree.right = Insert(tree.right, data);
if (Depth(tree.left) - Depth(tree.right) == -2) {
if (data > tree.right.data) {
// Insert at right child's right
// Left-Rotate
tree = RotateLeft(tree);
} else if (data < tree.right.data) {
// Insert at right child's left
// First Right-rotate on tree's right child
tree.right = RotateRight(tree.right);
// Then Left-rotate tree
tree = RotateLeft(tree);
}
}
}
}
// Update depth
tree.depth = Math.max(Depth(tree.left), Depth(tree.right)) + 1;
return tree;
}
public void Insert(int data) {
root = Insert(root, data);
}
private void Print(AVLNode tree) {
if (tree != null) {
Print(tree.left);
System.out.println(tree.data);
Print(tree.right);
}
}
public void Print() {
Print(root);
}
public boolean Find(int key) {
AVLNode ptr = root;
while (true) {
if (ptr == null) {
break;
}
if (key == ptr.data) {
return true;
} else if (key < ptr.data) {
ptr = ptr.left;
} else {
ptr = ptr.right;
}
}
return false;
}
private AVLNode root = null;
public static void main(String[] args) {
// AVLTree tree = new AVLTree();
// for (int i = 0; i < 1000; i++) {
// tree.Insert(i);
// }
// tree.Print();
// int key = 1000;
// System.out.println("Find: " + key + "? " + tree.Find(key));
// AVLTree tree = new AVLTree();
// int arr[] = { 13, 24, 37, 90, 53 };
// for (int data : arr) {
// tree.Insert(data);
// }
// tree.Print();
AVLTree tree = new AVLTree();
Random rand = new Random();
for (int i = 0; i < 10000; i++) {
tree.Insert(rand.nextInt(100000));
}
tree.Print();
}
}