无论是折半查找、二叉排序树查找还是B树,性能都依赖于查找中的比较次数。
一种理想情况是不经过任何比较,一次直接定位索要查找的记录,即:若数据结构中存在关键字和K相等,则其必定在f(K)的存储位置上,我们称这个对应关系f为哈希函数。
冲突(Collision):对不同的关键字,可能得到同一哈希地址,即存在key1!=key2,但f(key1)=f(key2)。此时称为冲突或碰撞。
由于在实际应用中,哈希函数都是压缩函数,所以冲突只能尽可能的减少,很难完全避免。
哈希表:根据设定的哈希函数H(key)和处理冲突的方法将一组关键字映像到一个有限的连续地址集合(区间)上,并以关键字在地址集合中的“像”作为记录在表中的位置,这种表称为哈希表,这一映像过程称为哈希造表或散列。所得的存储位置称为哈希地址或散列地址。
常见的哈希函数构造方法:
(1) 直接定址,如H(key) = a*key + b,如统计每个年龄的用户数。
(2) 数字分析,根据数据特点,取某一位或某几位叠加。
(3) 平方取中,取关键字平方后的中间几位(或平方)为哈希地址。
(4) 折叠法,将关键字纷呈几部分,然后每一部分的叠加和作为哈希地址。
(5) 除数余留法,取关键字被某个不大于哈希表长度的m的数p除后的余数,即算模 H(key) = key mod p。p的选择很重要,一般选质数或不包含小于20的质数因子的合数。
(6) 随机数法,利用伪随机特性,使用key作为种子,得到的随机数作为哈希地址。这个真有,比如Hadoop中某个Hash函数。
以上都是书上很陈旧的内容了,更为现代化的Hash函数请移步Wikipedia,List of Hash Functions。
我个人认为几个比较给力的是:BKDR(用于英文单词)、MurmerHash(速度最快的,针对X86优化CPU运算,基本纯位操作),据说Goog开发了CityHash也是借鉴MurmerHash,不知道效果怎么样。
下面说说处理冲突的方法:
(1) 开放定址法,H = (H(key)+d) mode m,其中d是发现冲突后,每次的增量。若d=1,2....则称作线性探测再散列;若d=1, -1, 4, -4....则叫做二次探测再散列;d也可以是随机数,称为随机探测再散列。注意,二次探测再散列只能在m=4j+3时才能使用!
(2) 再哈希法:H = RH(key)
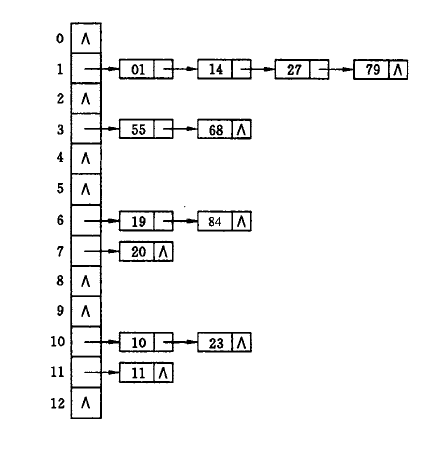
(3) 链地址法:将所有关键字为同一词的记录存储再同一线性链表中,拉链,如下图所示。
(4) 建立公共溢出区,不管哈希地址是什么,一旦发生冲突,都填入溢出表。个人觉得这个也很靠谱。
下面用Java实现了一个简单的哈希表,Hash函数是平方取模,冲突处理是线性探测再散列,使用cap=0.75判断是否需要重哈希,以减少冲突。
代码如下:
import java.util.ArrayList;
import java.util.Arrays;
public class HashTable {
public HashTable() {
// default capbility
cap = 10;
// default cnt
cnt = 0;
// default size
ht = new int[cap];
Arrays.fill(ht, Integer.MAX_VALUE);
// default load factor
lf = 0.75;
}
private int FindPos(int key) {
int pos = Hash(key);
while (ht[pos] != Integer.MAX_VALUE && ht[pos] != key) {
pos = (pos + 1) % cap; // 线性探测再散列
}
if (ht[pos] == key) {
return -1;
} else {
return pos;
}
}
private int Hash(int key) {
// A very simple & bad hash function
return (key * key) % cap;
}
private void ReHash() {
// System.out.println("Rehash");
// Simple * 2
int[] ht_old = ht;
cap *= 2;
ht = new int[cap];
Arrays.fill(ht, Integer.MAX_VALUE);
// Rehash all old key
for (int k : ht_old) {
if (k != Integer.MAX_VALUE) {
Insert(k);
}
}
}
public boolean Insert(int key) {
int pos = FindPos(key);
if (pos == -1) {
// Already in hash table
return false;
} else {
// Add to hash table
ht[pos] = key;
cnt++;
// Check if need to rehash
if ((double) cnt / cap > lf) {
ReHash();
}
return true;
}
}
public boolean Find(int key) {
int pos = FindPos(key);
if (pos == -1) {
return true;
} else {
return false;
}
}
/* Hash Table */
private int[] ht = null;
/* Load factor */
private double lf;
/* Capbility */
private int cap;
/* Cnt for actual elems */
private int cnt;
public static void main(String[] args) {
HashTable ht = new HashTable();
for (int i = 0; i < 100; i++) {
ht.Insert(i);
}
System.out.println(ht.Find(99));
}
}