前面实现的邻接矩阵面临一个巨大的问题：对于稀疏矩阵，将耗费巨大的资源，而大部分都是0。

现实中，绝大多数矩阵都是稀疏的！

我们可以采用如下的邻接表方法存储。

首先定义每个弧如下：

ivex是在顶点在数组中的下标。

next是一条链表，即某个顶点i的所有邻接结点的弧组成。

// Arc
struct Arc
{
	int ivex; // The vex position in vexs array
	struct Arc* next;
};

然后对于每个顶点，定义如下：

// Vex
struct Vex
{
	int data;
	struct Arc* first_arc;
};

因此，图可以如下表示：

// Graph
struct Graph
{
	struct Vex vexs[MAX_VEXS];
	int nvexs;
	int narcs;
};

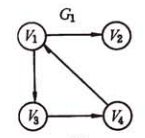
以书上的这个图为例：

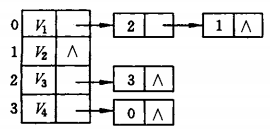
实际上用邻接表存储是如下效果：

邻接表上很容易找到任意一个顶点的第一个邻接点和下一个。这对于dfs、bfs等遍历很有优势。

但是要判定任意两个顶点vi和vj是否有边或者弧，必须搜索第i个和/或第j个链表，不如邻接矩阵方便。

BFS算法

BFS（Breadth First Search），又叫广度优先搜索。使得“先被访问的顶点的邻接点”限于“后被访问的顶点的邻接点”。

其实就是类似于树中的层次遍历，也是借助队列实现。

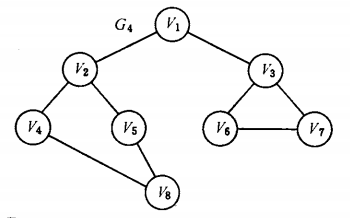
例如如下的图：

先访问v1，然后是v1的邻接点v2和v3，然后是v2的邻接点v4, v5，然后v3的邻接点。。。

最终次序：v1 -> v2 -> v3 -> v4 -> v5 -> v6 -> v7 -> v8

伪代码如下：

最终，使用循环队列+邻接表存储+BFS的代码如下：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_VEXS 100
#define MAX_QUEUE 1000

// Arc
struct Arc
{
	int ivex; // The vex position in vexs array
	struct Arc* next;
};

// Vex
struct Vex
{
	int data;
	struct Arc* first_arc;
};

// Graph
struct Graph
{
	struct Vex vexs[MAX_VEXS];
	int nvexs;
	int narcs;
};

int graph_locate(struct Graph* g, int val)
{
	int i;
	for(i=0; i<g->nvexs; i++)
	{
		if(g->vexs[i].data==val)
		{
			return i;
		}
	}
	return -1;
}

void graph_add_arc(struct Graph* g, int x, int y)
{
	// New arc
	struct Arc* new_arc = (struct Arc*)malloc(sizeof(struct Arc));
	struct Arc* ptr = NULL;
	if(!new_arc)
	{
		return ;
	}
	new_arc->ivex = y;
	new_arc->next = NULL;
	// Find vexs[x]'s tail
	if(!g->vexs[x].first_arc)
	{
		g->vexs[x].first_arc = new_arc;
	}else
	{
		ptr = g->vexs[x].first_arc;
		while(ptr->next!=NULL)
		{
			ptr = ptr->next;
		}
		ptr->next = new_arc;
	}
}

void graph_create(struct Graph* g)
{
	int i;
	int x, y;
	struct Arc* ptr;
	// Get n vexs
	printf("Please enter n for number of vexs:\n");
	scanf("%d", &g->nvexs);
	for(i=0; i<g->nvexs; i++)
	{
		printf("Please enter a int for vexs(%d):\n", i);
		scanf("%d", &g->vexs[i].data);
		g->vexs[i].first_arc = NULL;
	}
	// Get m arcs;
	printf("Please enter m for number of vexs:\n");
	scanf("%d", &g->narcs);
	for(i=0; i<g->narcs; i++)
	{
		printf("Please enter x y for arcs(%d):\n", i);
		scanf("%d %d", &x, &y);
		x = graph_locate(g, x);
		y = graph_locate(g, y);
		if(x==-1 || y==-1)
		{
			printf("Wrong x or y for arcs(%d).\n", i);
			i--;
		}
		// arc x->y
		graph_add_arc(g, x, y);
		// arc y->x
		graph_add_arc(g, y, x);
	}
}

void graph_print(struct Graph* g)
{
	int i;
	struct Arc* ptr;
	// Just print arcs
	for(i=0;i<g->nvexs;i++)
	{
		ptr = g->vexs[i].first_arc;
		while(ptr)
		{
			printf("%d->%d\n", g->vexs[i].data, g->vexs[ptr->ivex].data);
			ptr = ptr->next;
		}
	}
}

void graph_init(struct Graph* g)
{
	int i;
	for(i=0; i<MAX_VEXS; i++)
	{
		g->vexs[i].first_arc = NULL;
	}
	g->nvexs = 0;
	g->narcs = 0;
}

void graph_free(struct Graph* g)
{
	int i;
	struct Arc* ptr;
	struct Arc* free_node;
	g->nvexs = 0;
	g->narcs = 0;
	for(i=0; i<MAX_VEXS; i++)
	{
		ptr = g->vexs[i].first_arc;
		while(ptr!=NULL)
		{
			free_node = ptr;
			ptr = ptr->next;
			free(free_node);
		}
	}
}

struct Queue
{
	int data[MAX_QUEUE];
	int head;
	int rear;
};

void queue_init(struct Queue* q)
{
	q->head = 0;
	q->rear = 0;
}

int queue_is_full(struct Queue* q)
{
	return (q->rear+1)%MAX_QUEUE==q->head;
}

int queue_enqueue(struct Queue* q, int e)
{
	if(!queue_is_full(q))
	{
		q->data[q->rear] = e;
		q->rear = (q->rear+1) % MAX_QUEUE;
		return 0;
	}else
	{
		return -1;
	}
}

int queue_is_empty(struct Queue* q)
{
	return q->head==q->rear;
}

int queue_dequeue(struct Queue* q, int* e)
{
	if(!queue_is_empty(q))
	{
		*e = q->data[q->head];
		q->head = (q->head+1) % MAX_QUEUE;
		return 0;
	}else
	{
		return -1;
	}
}

void graph_visit(struct Graph* g, int i)
{
	printf("Visit %d\n", g->vexs[i].data);
}

void graph_bfs(struct Graph* g)
{
	int i, data;
	int flags[MAX_VEXS];
	struct Queue q;
	struct Arc* ptr;
	memset(flags, 0, sizeof(int)*MAX_VEXS);
	queue_init(&q);
	for(i=0; i<g->nvexs; i++)
	{
		if(!flags[i])
		{
			flags[i] = 1;
			graph_visit(g, i);
			queue_enqueue(&q, i);
			while(!queue_is_empty(&q))
			{
				queue_dequeue(&q, &data);
				ptr = g->vexs[data].first_arc;
				while(ptr!=NULL)
				{
					if(!flags[ptr->ivex])
					{
						flags[ptr->ivex] = 1;
						graph_visit(g, ptr->ivex);
						queue_enqueue(&q, ptr->ivex);
					}
					ptr = ptr->next;
				}
			}
		}
	}
}

int main()
{
	struct Graph g;
	graph_init(&g);
	graph_create(&g);
	//graph_print(&g);
	graph_bfs(&g);
	graph_free(&g);
	return 0;
}

测试数据：

8
1
2
3
4
5
6
7
8
9
1 2
1 3
2 4
2 5
5 8
4 8
3 6
3 7
6 7