一、后缀的定义
后缀数组,做为后缀树的替代品,可以解决很多棘手的字符串处理问题。
长度为n的String[0, 1...n-1]
定义后缀Suffix(i)=sub_string[i...n-1]。
例如字符串aabaaaab,Suffix[1] = abaaaab,Suffix[7]=b。
考虑到空间问题,以及C系列语言中,Suffix[i]非常好求得(&str[i]即可)。一般不会保存Suffix[i]这个数组。
二、后缀数组sa和逆运算数组rank。
后缀数组,一般写做sa,它的定义非常简单:将Suffix[i] i=0~n-1,按照字典序排序。
之后,sa[j]=i表示,排序后的第j位是Suffix[i]。
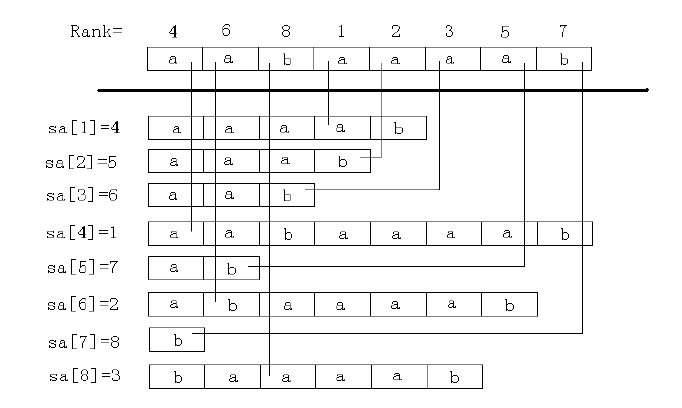
如下图所示:
名次数组:与sa数组对应的逆运算数组是排名数组rank。rank[i]=j,表示Suffix[i]在sa[j]中。
后缀数组说明:排名第几的是谁,名次数组说明:你排第几名。
三、后缀数组的算法:倍增算法(Doubling Algorithm)
表示看不懂思路,看不懂代码,只能借了模板,研究下输入、输出是什么……
基本思路:对每个字符开始的长度为2^k的子字符串进行排序,求出排名,即rank值,k从0开始,每次加1。
时间复杂度O(nlogn),空间复杂度6*n
输入参数如下:
r是要排序的字符串,一般为了方便处理,把字母转换到'a'~'z'之间。
sa是输出的后缀数组,其长度至少为len(r)。
n是r的长度。
m是r中数字的最大值范围。因为本算法内部用了基数排序。
此外,wa、wb、wv、ws是辅助
#include <stdio.h>
#include <string.h>
#define MAXN 100
int wa[MAXN],wb[MAXN],wv[MAXN],ws[MAXN];
int cmp(int *r,int a,int b,int l)
{
return r[a]==r[b]&&r[a+l]==r[b+l];
}
void da(int *r,int *sa,int n,int m)
{
int i,j,p,*x=wa,*y=wb,*t;
for(i=0;i<m;i++) ws[i]=0;
for(i=0;i<n;i++) ws[x[i]=r[i]]++;
for(i=1;i<m;i++) ws[i]+=ws[i-1];
for(i=n-1;i>=0;i--) sa[--ws[x[i]]]=i;
for(j=1,p=1;p<n;j*=2,m=p)
{
for(p=0,i=n-j;i<n;i++) y[p++]=i;
for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0;i<n;i++) wv[i]=x[y[i]];
for(i=0;i<m;i++) ws[i]=0;
for(i=0;i<n;i++) ws[wv[i]]++;
for(i=1;i<m;i++) ws[i]+=ws[i-1];
for(i=n-1;i>=0;i--) sa[--ws[wv[i]]]=y[i];
for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
}
return;
}
int main()
{
char* str = "aabaaaab";
int sa[MAXN];
int str_i[MAXN];
int i;
int len = strlen(str);
// Process ascii string to 'a'~'z', cut range to < 30
for(i=0; i<len; i++)
{
str_i[i] = str[i] - 'a';
}
da(str_i, sa, len, 30);
for(i=0; i<len; i++)
{
printf("Rank %d, Suffix %s\n", i, &str[sa[i]]);
}
return 0;
}
输出如下:
Rank 0, Suffix aaaab Rank 1, Suffix aaab Rank 2, Suffix aab Rank 3, Suffix aabaaaab Rank 4, Suffix ab Rank 5, Suffix abaaaab Rank 6, Suffix b Rank 7, Suffix baaaab
四、后缀数组的算法:DC3
本算法时间复杂度为O(nlogn),空间复杂度10*n。是03年新提出的算法。
DC3算法区别于DA算法:s、sa数组都必须是3的倍数。
如果s不够,需要补len(s)-3n个0到达len_3n,而且结果数组sa中前len_3n-len个字符会是0。即从len_3n-len开始才是正式的sa数组。
代码如下:
#include <string.h>
#include <stdio.h>
#define MAXN 100
#define F(x) ((x)/3+((x)%3==1?0:tb))
#define G(x) ((x)<tb?(x)*3+1:((x)-tb)*3+2)
int wa[MAXN],wb[MAXN],wv[MAXN],ws[MAXN];
int c0(int *r,int a,int b)
{return r[a]==r[b]&&r[a+1]==r[b+1]&&r[a+2]==r[b+2];}
int c12(int k,int *r,int a,int b)
{if(k==2) return r[a]<r[b]||r[a]==r[b]&&c12(1,r,a+1,b+1);
else return r[a]<r[b]||r[a]==r[b]&&wv[a+1]<wv[b+1];}
void sort(int *r,int *a,int *b,int n,int m)
{
int i;
for(i=0;i<n;i++) wv[i]=r[a[i]];
for(i=0;i<m;i++) ws[i]=0;
for(i=0;i<n;i++) ws[wv[i]]++;
for(i=1;i<m;i++) ws[i]+=ws[i-1];
for(i=n-1;i>=0;i--) b[--ws[wv[i]]]=a[i];
return;
}
void dc3(int *r,int *sa,int n,int m)
{
int i,j,*rn=r+n,*san=sa+n,ta=0,tb=(n+1)/3,tbc=0,p;
r[n]=r[n+1]=0;
for(i=0;i<n;i++) if(i%3!=0) wa[tbc++]=i;
sort(r+2,wa,wb,tbc,m);
sort(r+1,wb,wa,tbc,m);
sort(r,wa,wb,tbc,m);
for(p=1,rn[F(wb[0])]=0,i=1;i<tbc;i++)
rn[F(wb[i])]=c0(r,wb[i-1],wb[i])?p-1:p++;
if(p<tbc) dc3(rn,san,tbc,p);
else for(i=0;i<tbc;i++)
san[rn[i]]=i;
for(i=0;i<tbc;i++)
if(san[i]<tb)
wb[ta++]=san[i]*3;
if(n%3==1)
wb[ta++]=n-1;
sort(r,wb,wa,ta,m);
for(i=0;i<tbc;i++)
wv[wb[i]=G(san[i])]=i;
for(i=0,j=0,p=0;i<ta
&&
j<tbc;p++)
sa[p]=c12(wb[j]%3,r,wa[i],wb[j])?wa[i++]:wb[j++];
for(;i<ta;p++)
sa[p]=wa[i++];
for(;j<tbc;p++)
sa[p]=wb[j++];
return;
}
int main()
{
char* str = "aabaaaab";
int sa[MAXN];
int str_i[MAXN];
int i;
int len = strlen(str);
int len_3n = 0;
// Process ascii string to 'a'~'z', cut range to < 30
for(i=0; i<len; i++)
{
str_i[i] = str[i] - 'a'+1;
}
// Append r's len to 3n
len_3n = len;
while(len_3n%3) {
str_i[len_3n++] = 0;
}
dc3(str_i, sa, len_3n, 27);
for(i=(len_3n-len); i<len_3n; i++)
{
printf("Rank %d, Suffix %s\n", i-(len_3n-len), &str[sa[i]]);
}
return 0;
}
输出:
Rank 0, Suffix aaaab Rank 1, Suffix aaab Rank 2, Suffix aab Rank 3, Suffix aabaaaab Rank 4, Suffix ab Rank 5, Suffix abaaaab Rank 6, Suffix b Rank 7, Suffix baaaab
本文只讲述了基础的后缀数组sa的算法,具体到应用问题,一般还要结合另外一个数组height,改日再续……
上边dc3的代码有bug,在进行SA0和SA12 的merge之前应该将r数组的n位后的内容置0,否则在比较过程中可能出错。
bug的证明:测试样例:char str="aaaaaa";