一、后缀的定义
后缀数组，做为后缀树的替代品，可以解决很多棘手的字符串处理问题。
长度为n的String[0, 1...n-1]
定义后缀Suffix(i)=sub_string[i...n-1]。
例如字符串aabaaaab，Suffix[1] = abaaaab，Suffix[7]=b。
考虑到空间问题，以及C系列语言中，Suffix[i]非常好求得（&str[i]即可）。一般不会保存Suffix[i]这个数组。
二、后缀数组sa和逆运算数组ran[......]
问题描述
要求从N个元素中随机的抽取k个元素，其中N无法确定(N是个流，可能无穷大)。
这种应用的场景一般是数据流的情况下，由于数据只能被读取一次，而且数据量很大，并不能全部保存，因此数据量N是无法在抽样开始时确定的；但又要保持随机性，于是有了这个问题。所以搜索网站有时候会问这样的问题。
这里的核心问题就是“随机”，怎么才能是随机的抽取元素呢？我们设想，买彩票的时候，由于所有彩票的中奖概率都是一样的，所以我们才是“随机的”买彩票。那么要使抽取数据也随机，必须使每一个数据被抽样出[......]
键树，又称数字查找树(Digital Search Trees)是一棵度>=2的树，每个结点只含有组成关键字的符号。
键树有两种存储结构：
1、树的孩子-兄弟链表来表示键树。
每个Node有三个域：first指向第一棵子树的根指针；next指向右兄弟；info（可选的）记录附加数据。如下图：
查找过程是，从根结点出发，顺着first查找，如果相等，继续下一个first。否则沿着next查找。直到到了空指针为止。此时若仍未完成key的匹配，查找不成功。[......]
本文是转载的，《B树、B-树、B+树、B*树》
B树
即二叉搜索树：
1.所有非叶子结点至多拥有两个儿子（Left和Right）；
2.所有结点存储一个关键字；
3.非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；
如：
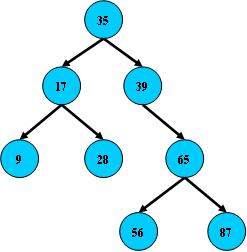B树的搜索，从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；
否则，如果查询关键字比结点关键字小，就进入左儿子；如果比结点关键字大，就进入右儿子；如果左儿子或右儿子的指针为空，则报告找不到相应的关键字[......]
大二那会根本没蹋下心来看，觉得天书一般，连旋转都没搞明白。
今天仔细看了书，发现真的一点不难啊，鄙视自己……
首先是概念：
平衡二叉树是为了解决前面二叉排序树不均衡的问题，而加入了一种平衡机制。所以，平衡二叉树是一种特殊的二叉排序树(BST)！
AVL树查找的平均和最差复杂度都是O(logn) ！！！(BST的最坏是O(n))
AVL树的插入复杂度是O(logn)。
平衡二叉树（简称AVL树）：对任意一个结点，它的左子树和又子树都是平衡二叉树（左子树都小于结点[......]