DAG和概念

有向无环图：顾名思义，有向图，且不含环，directed acycline graph，简称DAG图。

无向图检查环：若深度优先遍历过程遇到回边（先前访问过的顶点的边），则必定存在环。

有向图检查环：从某个顶点v出发，在dfs(v)结束前，出现一条从顶点u到顶点v的回边，由于u在生成树上是v的子孙，则有向图必定存在包含顶点v和u之间的环。

DAG图是描述工程的有效工具。一个工程可以用一个DAG图表示，每一个顶点是一个子工程，工程的先后关系用弧表示。

围绕着工程，两个关心的问题是：

1、工程能否顺利进行（拓扑排序问题）

2、工程完成所必须的最短时间（关键路径问题）

 

AOV网和拓扑排序

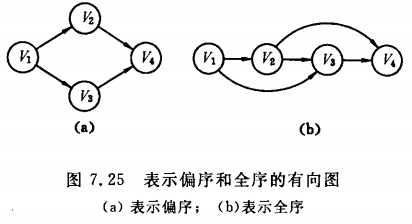
偏序：集合中仅有部分成员之间可以比较。

全序：集合中全体成员均可比较。

比如下图左边是偏序，右边是全序。

拓扑有序：全序上面的排序

拓扑排序：由于集合上一个偏序得到该集合上的一个全序。

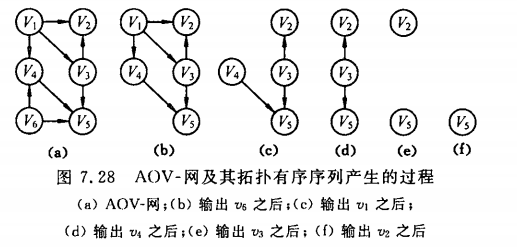
AOV网(Activity On Vertex Network)：用顶点表示活动，用弧表示活动之间的优先关系的有向图称为顶点表示活动的网。

在AOV网上不应该出现有向环，因此，给定一个AOV网，要先判断是否存在环。

AOV图求拓扑排序的算法如下：

1、从有向图中选取一个没有前驱的顶点（入度为0的）。

2、从图中删除该顶点和所有以它为尾的弧(此时可能会产生新的无前驱顶点)。

循环上述两步，直到

(1)所有顶点都全部输出。

Or

(2)不存在无前驱的顶点，说明图中有环。

上述算法非常简单明了，连AOV图的环判定也一起做了。

具体到实现，我们可以增添两个数据结构：

(1) 存放各个顶点入度的集合indegree。

(2)一个暂存入度为0的栈。

算法变成了：

1、扫描所有顶点的入度。

2、将入度为0的，入栈。

3、循环直到栈空

弹出栈、输出。

将关联的边入度减1，如果为0，入栈。

4、最终检查输出了多少个结点，如果小于nvexs，说明有环。

代码如下：

注意这里是有向图，图的创建不能在用无向图的双边了！

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_VEXS 100
#define MAX_QUEUE 1000

// Arc
struct Arc
{
	int ivex; // The vex position in vexs array
	struct Arc* next;
};

// Vex
struct Vex
{
	int data;
	struct Arc* first_arc;
};

// Graph
struct Graph
{
	struct Vex vexs[MAX_VEXS];
	int nvexs;
	int narcs;
};

int graph_locate(struct Graph* g, int val)
{
	int i;
	for(i=0; i<g->nvexs; i++)
	{
		if(g->vexs[i].data==val)
		{
			return i;
		}
	}
	return -1;
}

void graph_add_arc(struct Graph* g, int x, int y)
{
	// New arc
	struct Arc* new_arc = (struct Arc*)malloc(sizeof(struct Arc));
	struct Arc* ptr = NULL;
	if(!new_arc)
	{
		return ;
	}
	new_arc->ivex = y;
	new_arc->next = NULL;
	// Find vexs[x]'s tail
	if(!g->vexs[x].first_arc)
	{
		g->vexs[x].first_arc = new_arc;
	}else
	{
		ptr = g->vexs[x].first_arc;
		while(ptr->next!=NULL)
		{
			ptr = ptr->next;
		}
		ptr->next = new_arc;
	}
}

void graph_create(struct Graph* g)
{
	int i;
	int x, y;
	struct Arc* ptr;
	// Get n vexs
	printf("Please enter n for number of vexs:\n");
	scanf("%d", &g->nvexs);
	for(i=0; i<g->nvexs; i++)
	{
		printf("Please enter a int for vexs(%d):\n", i);
		scanf("%d", &g->vexs[i].data);
		g->vexs[i].first_arc = NULL;
	}
	// Get m arcs;
	printf("Please enter m for number of vexs:\n");
	scanf("%d", &g->narcs);
	for(i=0; i<g->narcs; i++)
	{
		printf("Please enter x y for arcs(%d):\n", i);
		scanf("%d %d", &x, &y);
		x = graph_locate(g, x);
		y = graph_locate(g, y);
		if(x==-1 || y==-1)
		{
			printf("Wrong x or y for arcs(%d).\n", i);
			i--;
		}
		// arc x->y
		graph_add_arc(g, x, y);
	}
}

void graph_print(struct Graph* g)
{
	int i;
	struct Arc* ptr;
	// Just print arcs
	for(i=0;i<g->nvexs;i++)
	{
		ptr = g->vexs[i].first_arc;
		while(ptr)
		{
			printf("%d->%d\n", g->vexs[i].data, g->vexs[ptr->ivex].data);
			ptr = ptr->next;
		}
	}
}

void graph_init(struct Graph* g)
{
	int i;
	for(i=0; i<MAX_VEXS; i++)
	{
		g->vexs[i].first_arc = NULL;
	}
	g->nvexs = 0;
	g->narcs = 0;
}

void graph_free(struct Graph* g)
{
	int i;
	struct Arc* ptr;
	struct Arc* free_node;
	g->nvexs = 0;
	g->narcs = 0;
	for(i=0; i<MAX_VEXS; i++)
	{
		ptr = g->vexs[i].first_arc;
		while(ptr!=NULL)
		{
			free_node = ptr;
			ptr = ptr->next;
			free(free_node);
		}
	}
}

#define MAX_STACK 100

struct Stack
{
	int top;
	int data[MAX_STACK];
};

void stack_init(struct Stack* stk)
{
	stk->top = 0;
}

int stack_push(struct Stack* stk, int v)
{
	if(stk->top>=MAX_STACK)
	{
		return -1;
	}else
	{
		stk->data[stk->top++] = v;
		return 0;
	}
}

int stack_pop(struct Stack* stk, int* v)
{
	if(stk->top==0)
	{
		return -1;
	}else
	{
		*v = stk->data[--stk->top];
		return 0;
	}
}

int stack_is_empty(struct Stack* stk)
{
	return stk->top==0;
}

void topo_sort(struct Graph* g)
{
	// Count indegree for all vex
	int* indeg = (int*)malloc(sizeof(int)*g->nvexs);
	int i;
	int cnt = 0;
	struct Arc* ptr = NULL;
	for(i=0;i<g->nvexs;i++)
	{
		indeg[i] = 0;
	}
	for(i=0;i<g->nvexs;i++)
	{
		ptr = g->vexs[i].first_arc;
		while(ptr!=NULL)
		{
			indeg[ptr->ivex]++;
			ptr = ptr->next;
		}
	}
	// Stack push all 0-indegree
	struct Stack* stk = (struct Stack*)(malloc(sizeof(struct Stack)));
	stack_init(stk);
	for(i=0;i<g->nvexs;i++)
	{
		if(indeg[i]==0)
		{
			if(-1==stack_push(stk, i))
			{
				printf("Push fail...\n");
				break;
			}
		}
	}
	// While !stack.empty()
	while(!stack_is_empty(stk))
	{
		int tmp;
		if(-1==stack_pop(stk, &tmp))
		{
			printf("Pop fail...\n");
			break;
		}else
		{
			// Output an vex
			printf("%d\n", g->vexs[tmp].data);
			cnt++;
			// Count-- for every vex[tmp]'s neigbhour
			ptr = g->vexs[tmp].first_arc;
			while(ptr!=NULL)
			{
				if(--indeg[ptr->ivex]==0)
				{
					stack_push(stk, ptr->ivex);
				}
				ptr = ptr->next;
			}
		}
	}
	// Free malloc resource
	free(stk);
	free(indeg);
	if(cnt<g->nvexs)
	{
		printf("This graph has cycle!!!\n");
	}
}

int main()
{
	struct Graph g;
	graph_init(&g);
	graph_create(&g);
	topo_sort(&g);
	graph_free(&g);
	return 0;
}

测试的AVO图：

测试数据：

6
1
2
3
4
5
6
8
1 2
1 3
1 4
3 2
3 5
4 5
6 4
6 5

测试输出：

6  1  4  3  5  2