数据结构重读 - AOV网和关键路径

Leave a reply

与AOV网对应的，还有一个AOE网，当然它也是有DAG(向无环图)。

AOE(Activity On Edge)网：顾名思义，用边表示活动的网。

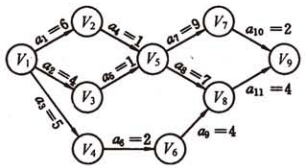
与AOV不同，活动都表示在了边上，如下图所示：

如上所示，共有11项活动（11条边），9个事件（9个顶点）。

整个工程只有一个开始点和一个完成点。

即只有一个入度为零的点（源点）和只有一个出度为零的点（汇点）。

(1) 关键路径：是从开始点到完成点的最长路径的长度。路径的长度是边上活动耗费的时间。

(2) 最早发生时间：v1到vi的最长路径叫做vi的最早发生时间，用ei表示。例如上图中，v5的最早发生时间是max(6+1, 4+1) = 7。

(3) 最迟开始时间：在不推迟整个工程完成的前提下，活动i最迟必须开始进行的时间，用l(i)表示。l(i) - e(i)是活动的时间余量。

(4) 关键活动：l(i)=e(i)的活动称为关键活动。

关键路径上的活动都是关键活动。

提前完成非关键活动并不能加快工程进度（类似木桶效应）。

AOE网的主要活动就是识别出哪些是关键活动，以便争取提高关键活动的工效，缩短整个工期。

当然，如果AOE网发生了改变，那么原先的关键路径也会发生变化。

因此，只有在不改变挂件路径的情况下，提供关键活动的速度，才能对整体工程进度起到帮助作用。

求关键路径的算法

求关键路径，就是要求e(i) = l(i)的事件(点)。我们首先必须分别求出所有点的e(i)和l(i)。

由于ve和vl的递推公式必须在拓扑排序下有效，因此，先要求拓扑排序

0、求拓扑排序(同时顺道求ve)

要增设一个栈T记录拓扑有序序列，计算求得各个顶点的ve之后，从栈顶依次弹出栈，就可以倒序遍历，求vl了。

还要使用拓扑排序的那个入度为0的栈，可以每次Pop时候顺道记录下，最后cnt如果<g->nvexs，则表示有环。

1、求最早发生时间ve[]

ve(0)=0开始递推

ve(j) = max{ve{i}+dut(i, j)}

2、求最晚发生时间vl[]

从vl(n-1)=ve(n-1)开始倒推。

vl(j) = min{vl(i) - dut(j, i)}。

3、遍历，求出ve(i) = vl(i)的所有点i。

算法总时间复杂度是O(n+e)。

具体的代码如下：

求拓扑排序和ve、以及栈T

void topo_sort_ve(struct Graph* g, struct Stack* tstk, int* ve)
{
	// Malloc
	int* indeg = (int*)malloc(sizeof(int)*g->nvexs);
	int i = 0;
	int j;
	int cnt = 0;
	struct Arc* ptr = NULL;
	struct Stack* stk = (struct Stack*)malloc(sizeof(struct Stack));

	// Init stk
	stack_init(stk);

	// Compute indegree
	memset(indeg, 0, sizeof(int)*g->nvexs);
	for(i=0; i<g->nvexs; i++)
	{
		ptr = g->vexs[i].first_arc;
		while(ptr!=NULL)
		{
			indeg[ptr->ivex]++;
			ptr = ptr->next;
		}
	}

	// Push all vex that indeg is 0
	for(i=0; i<g->nvexs; i++)
	{
		if(indeg[i]==0)
		{
			if(-1==stack_push(stk, i))
			{
				printf("Stack push fail.\n");
				return ;
			}
		}
	}

	// while ! stk.empty
	memset(ve, 0, sizeof(int)*g->nvexs);
	while(!stack_is_empty(stk))
	{
		// Pop
		if(-1==stack_pop(stk, &j))
		{
			printf("Stack pop fail.\n");
			return ;
		}
		// Topo stk
		if(-1==stack_push(tstk, j))
		{
			printf("Stack push fail.\n");
			return ;
		}
		// Cnt
		cnt++;
		// Process all neghbour
		ptr = g->vexs[j].first_arc;
		while(ptr!=NULL)
		{
			// Push if indegree change to zero
			if(--indeg[ptr->ivex]==0)
			{
				stack_push(stk, ptr->ivex);
			}
			// ve[k] = max(e(j) arc(j, k))
			if(ve[j] + ptr->w > ve[ptr->ivex])
			{
				ve[ptr->ivex] = ve[j] + ptr->w;
			}
			ptr = ptr->next;
		}
	}

	// Free
	free(indeg);
	free(stk);

	// Cnt to see if has cycle
	if(cnt<g->nvexs)
	{
		printf("Has Cycle!\n");
	}
	return ;
}

求vl

void topo_vl(struct Graph* g, struct Stack* tstk, int* ve, int* vl)
{
	int i;
	int j;
	struct Arc* ptr = NULL;
	// Pop end point
	if(-1==stack_pop(tstk, &j))
	{
		printf("Pop fail.\n");
		return ;
	}
	for(i=0; i<g->nvexs; i++)
	{
		vl[i] = ve[j];
	}
	// while ! empty
	while(!stack_is_empty(tstk))
	{
		// Pop j
		if(-1==stack_pop(tstk, &j))
		{
			printf("Pop fail.\n");
			return ;
		}
		// vl[j] = min(vl[k]-arc(j,k)), k is ptr->ivex
		ptr =  g->vexs[j].first_arc;
		while(ptr!=NULL)
		{
			if(vl[ptr->ivex] - ptr->w < vl[j])
			{
				vl[j] = vl[ptr->ivex] - ptr->w;
			}
			ptr = ptr->next;
		}
	}
	return ;
}

求关键路径

void critical_path(struct Graph* g, int* ve, int* vl)
{
	int i;
	printf("Critical Path:");
	for(i=0;i<g->nvexs;i++)
	{
		if(ve[i]==vl[i])
		{
			printf("%d ", g->vexs[i].data);
		}
	}
	printf("\n");
}

其他代码，如创建等，注意我们要存储活动的耗费，给Arc加了一个权值w。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_VEXS 100
#define MAX_QUEUE 1000

// Arc
struct Arc
{
	int ivex; // The vex position in vexs array
	int w; // The data on arc(path)
	struct Arc* next;
};

// Vex
struct Vex
{
	int data;
	struct Arc* first_arc;
};

// Graph
struct Graph
{
	struct Vex vexs[MAX_VEXS];
	int nvexs;
	int narcs;
};

int graph_locate(struct Graph* g, int val)
{
	int i;
	for(i=0; i<g->nvexs; i++)
	{
		if(g->vexs[i].data==val)
		{
			return i;
		}
	}
	return -1;
}

void graph_add_arc(struct Graph* g, int x, int y, int w)
{
	// New arc
	struct Arc* new_arc = (struct Arc*)malloc(sizeof(struct Arc));
	struct Arc* ptr = NULL;
	if(!new_arc)
	{
		return ;
	}
	new_arc->ivex = y;
	new_arc->w = w;
	new_arc->next = NULL;
	// Find vexs[x]'s tail
	if(!g->vexs[x].first_arc)
	{
		g->vexs[x].first_arc = new_arc;
	}else
	{
		ptr = g->vexs[x].first_arc;
		while(ptr->next!=NULL)
		{
			ptr = ptr->next;
		}
		ptr->next = new_arc;
	}
}

void graph_create(struct Graph* g)
{
	int i;
	int x, y, w;
	struct Arc* ptr;
	// Get n vexs
	printf("Please enter n for number of vexs:\n");
	scanf("%d", &g->nvexs);
	for(i=0; i<g->nvexs; i++)
	{
		printf("Please enter a int for vexs(%d):\n", i);
		scanf("%d", &g->vexs[i].data);
		g->vexs[i].first_arc = NULL;
	}
	// Get m arcs;
	printf("Please enter m for number of vexs:\n");
	scanf("%d", &g->narcs);
	for(i=0; i<g->narcs; i++)
	{
		printf("Please enter x y w for arcs(%d):\n", i);
		scanf("%d %d %d", &x, &y, &w);
		x = graph_locate(g, x);
		y = graph_locate(g, y);
		if(x==-1 || y==-1)
		{
			printf("Wrong x or y for arcs(%d).\n", i);
			i--;
		}
		// arc x->y
		graph_add_arc(g, x, y, w);
	}
}

void graph_print(struct Graph* g)
{
	int i;
	struct Arc* ptr;
	// Just print arcs
	for(i=0;i<g->nvexs;i++)
	{
		ptr = g->vexs[i].first_arc;
		while(ptr)
		{
			printf("%d->%d\n", g->vexs[i].data, g->vexs[ptr->ivex].data);
			ptr = ptr->next;
		}
	}
}

void graph_init(struct Graph* g)
{
	int i;
	for(i=0; i<MAX_VEXS; i++)
	{
		g->vexs[i].first_arc = NULL;
	}
	g->nvexs = 0;
	g->narcs = 0;
}

void graph_free(struct Graph* g)
{
	int i;
	struct Arc* ptr;
	struct Arc* free_node;
	g->nvexs = 0;
	g->narcs = 0;
	for(i=0; i<MAX_VEXS; i++)
	{
		ptr = g->vexs[i].first_arc;
		while(ptr!=NULL)
		{
			free_node = ptr;
			ptr = ptr->next;
			free(free_node);
		}
	}
}

#define MAX_STACK 100

struct Stack
{
	int top;
	int data[MAX_STACK];
};

void stack_init(struct Stack* stk)
{
	stk->top = 0;
}

int stack_push(struct Stack* stk, int v)
{
	if(stk->top>=MAX_STACK)
	{
		return -1;
	}else
	{
		stk->data[stk->top++] = v;
		return 0;
	}
}

int stack_pop(struct Stack* stk, int* v)
{
	if(stk->top==0)
	{
		return -1;
	}else
	{
		*v = stk->data[--stk->top];
		return 0;
	}
}

int stack_is_empty(struct Stack* stk)
{
	return stk->top==0;
}

测试驱动：

int main()
{
	struct Graph g;
	struct Stack tstk;
	int ve[MAX_VEXS];
	int vl[MAX_VEXS];
	int i;
	graph_init(&g);
	graph_create(&g);
	stack_init(&tstk);
	topo_sort_ve(&g, &tstk, ve);
	//for(i=0;i<g.nvexs;i++)
	//{
	//	printf("%d\n", ve[i]);
	//}
	topo_vl(&g, &tstk, ve, vl);
	//for(i=0;i<g.nvexs;i++)
	//{
	//	printf("%d\n", vl[i]);
	//}
	critical_path(&g, ve, vl);
	graph_free(&g);
	return 0;
}

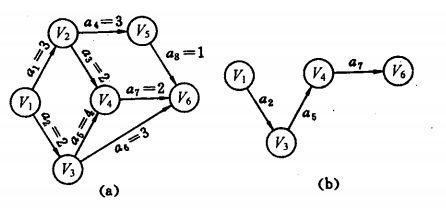
测试AOE图：

测试数据：

6
1
2
3
4
5
6
8
1 2 3
1 3 2
2 4 2
3 4 4
2 5 3
5 6 1
4 6 2
3 6 3

测试输出：

Critical Path:1 3 4 6

 

 

您可能也喜欢如下文章:

  1. 数据结构重读 - 有向无环图、AOV网和拓扑排序
  2. 数据结构重读 - 图的链式存储(邻接表)和BFS图遍历算法
  3. 数据结构重读 - 图的遍历(概念)
  4. 数据结构重读 – 栈的基本操作
  5. 数据结构重读 - 关节点(割点)和重连通分量

Leave a Reply

Your email address will not be published. Required fields are marked *